
对于科研人员而言,实验完成后最重要的任务之一就是对数据进行恰当的分析。无论你是从事基础研究、临床研究,还是社会科学,只要实验中涉及变量比较,就绕不开一个核心问题:我该选择哪种统计检验方法?在日常科研中,我们经常遇到这样的困惑:到底应该用T检验,还是ANOVA?是选择参数检验,还是非参数检验?面对复杂的实验设计和多样的数据类型,一张清晰的统计检验决策图往往能帮助我们快速理清思路,从源头上避免统计方法选用错误带来的后续麻烦。
我们在LaNts and Laminins网站上看到了一张非常实用的流程图:
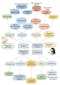
我们就以这张统计检验流程图为基础,系统梳理科研数据分析中常见的统计方法选择路径。我们将从变量类型入手,逐步过渡到实验设计的不同情形,再进一步探讨各种统计方法的适用条件与逻辑思路,帮助你从源头上建立对“统计方法选择”这件事的系统认识。记得收藏哦~~
以因变量为起点:你在比较什么?
任何一项统计分析的出发点,都是因变量(dependent variable),也就是你最终希望检验的“结果变量”。在实际研究中,因变量可能是分类变量,例如样本是否患病,是否发生某种行为;也可能是连续变量,如血压水平、反应时间、基因表达量等;甚至可能是多个连续变量的组合,如不同基因在多个时间点的表达谱,这类情况需要对多个变量同时进行分析。
因此,第一步就是明确你的因变量属于哪一类。分类变量通常涉及频数或比例的比较,连续变量则用于均值、方差、趋势等数值属性的比较。当你面对的是多个连续因变量时,例如多个行为评分或多项生理指标,就需要考虑使用多变量分析方法(如MANOVA),以避免多重比较带来的第一类错误(Type I error)膨胀。
接着看自变量:你的实验是如何设计的?
在确认因变量后,第二个关键问题是你的实验设计如何安排,也就是自变量(independent variable)的结构和特征。这包括几个重要维度:
首先要判断的是实验组的数量。是两个组之间的比较,还是三个及以上组?比如,如果你有一个对照组和一个干预组,就属于双组设计;如果有低、中、高剂量三个处理组,那就是多组设计,所采用的统计方法自然会不同。
其次,要判断组间是否为独立设计。独立组意味着不同的受试对象被随机分配到不同组别,如两批不同人接受不同药物处理;而非独立设计(又称配对设计或重复测量设计)则意味着同一组受试对象在多个时间点或条件下反复测量,如同一个人在干预前后分别测量血压。
还有一个重要维度是数据是否经过标准化或归一化处理。在一些生物实验中,原始数据可能存在较大个体差异,此时研究者往往采用“内部归一化”方法,如将表达量归一化为百分比、变化倍数或相对表达值。这种处理会影响后续统计方法的选择,尤其在方差分析中,需特别注意各组方差是否齐性(homogeneity of variance)。
从方法选择角度解读常见情形
当因变量是分类变量时,研究者往往需要比较两组或多组之间的频数差异。例如,某项干预是否能显著提高行为发生的比例,是否能减少某种不良事件的发生率等。在这种情况下,如果你要检验两个分类变量之间是否独立,最常用的方法就是卡方检验(Chi-square test)。如果你的因变量和自变量都是分类变量,且都含有两个以上水平,则可进一步使用对分类数据建模的Loglinear分析,以探讨变量之间的交互作用。
若因变量是连续变量,而你只比较两个独立组之间的差异,最常用的是独立样本T检验(Independent T-test)。如果是同一组个体在不同时间点的比较,配对T检验(Paired T-test)更为合适。值得注意的是,当数据不满足正态分布的假设时,这两种T检验的非参数替代方法分别是Mann-Whitney U检验和Wilcoxon配对秩和检验。
在多组比较情形下,单因素方差分析(One-way ANOVA)用于三个及以上独立组之间的均值比较,而若是重复测量情境(例如不同时间点下的相同受试对象),则需要采用重复测量方差分析(Repeated Measures ANOVA)。当数据不符合正态分布时,可考虑其非参数对应方法:Kruskal-Wallis检验(独立组)和Friedman检验(重复测量组)。
多因子设计与多变量响应:向复杂性进阶
很多实验并不仅仅涉及一个因素。比如,你可能同时考察“性别”和“治疗方式”对某种行为的影响,这就属于双因素设计。此时应使用双因素方差分析(Two-way ANOVA)或交互效应分析(Factorial ANOVA),以评估两个因素及其交互作用对因变量的影响。
更进一步,如果你的实验中测量了多个连续因变量,比如既测量反应时间、也测量准确率,同时希望比较它们在不同组别之间的差异,那么就应使用多变量方差分析(MANOVA)。MANOVA不仅能比较组间均值,还能控制变量间的协方差结构,从而提供更为综合的分析视角。
连续变量间的关系分析:相关与回归的应用
除了组间差异分析,科研中还经常需要探索变量之间的相关性。例如,基因表达水平与疾病严重程度之间的关系,或者睡眠时间与注意力表现之间的相关程度。此时应考虑使用相关分析(Correlation)或回归分析(Regression)。
Pearson相关系数是连续变量之间线性关系的标准衡量指标,适用于数据服从正态分布的情形;当数据偏离正态分布,或者为等级变量时,可以选择Spearman秩相关系数。若希望进一步预测一个变量对另一个变量的影响,线性回归是常用方法。若因变量是二分类变量(如是否患病),则应使用Logistic回归建模,其优点在于不仅能估计变量之间的关联强度,还可计算事件发生的概率。
用一张图建立“统计决策树”思维
这张统计检验流程图最大的价值在于,它把研究设计、变量类型、数据特征等要素整合到一个系统的判断路径中,使我们可以从整体上理解统计方法的“选择逻辑”。而不是像以往那样,把各种方法当作孤立的工具,而是在面对具体问题时,能够反推自己是否具备使用该方法的前提条件。
许多科研人员在投稿阶段常被评审人质疑统计分析是否得当,往往正是因为未能在分析前就理清实验设计与方法匹配关系,导致方法使用不当或数据解读偏差。而这张图所提供的结构化思维框架,正是解决这一问题的有效路径。
写在最后:统计分析是科研设计的延伸
统计方法的选择,不应只在数据分析阶段才考虑。优秀的研究设计往往在实验前就已预设了合理的统计方案。本文所讲述的判断流程,可以作为一套“提前规划”的工具,帮助科研人员在设计实验时就明确数据结构与后续分析的契合度。只有如此,我们才能从方法论层面提升研究的严谨性、可重复性与说服力。
关于统计分析方法,你也可以看看AJE其他相关文章:
